How Blockchain Ledger Models Affect Transactions and Security

Table of Links

Abstract and I. Introduction

II. Background

III. Related Works

IV. Comparative Analysis

V. Findings and Evaluation

VI. Conclusion and References

II. BACKGROUND

A. Ledger State

At a high level, blockchains can be seen as state machines, which are used to permanently and immutably record the change in the state of the ledger. A state machine is a mathematical model which represents a machine with exactly one state at any time, capable of transitioning to a new state based on external interactions and documenting previous states [3]. The two main models used to represent how the state is recorded are Unspent Transaction Outputs (UTXO) and Account-based The UTXO model performs local and deterministic state management through the set of all transaction outputs stored within a ledger and is most notably used by Bitcoin. Following a newly created transaction, UTXOs are generated from the output to represent the value transferred and are then assigned to the receiver’s public address. A user can use any UTXOs that are assigned to their private key for further transactions, but once the transaction is verified and stored in the ledger, the UTXO will be considered spent and is no longer usable. This model does not incorporate accounts at the protocol level but uses wallets to maintain balance by recording the sum of all UTXOs for an account [4]. The account-based model tracks the global shared state of asset balances for all accounts on the network, with the Ethereum blockchain following this state model. The two account types seen in this model are the private-key user accounts and global smart contract accounts, both of which contain executable code, account balance and internal memory. When a transaction is sent and verified on the ledger, the sender’s balance is decreased and the receiving account balance is increased by the same value. After a transaction has occurred, the global state is updated to reflect any changes to account balance [5]. The UTXO model maintains simple and deterministic state in distributed and concurrency computing environments, but is limited in functionality to execute expressive scripts. In contrast, the account ledger is focused on completely expressive smart contracts on a global shared state. IOHK proposed the Extended UTXO model, which builds upon Bitcoin’s UTXO model to maintain the inherent semantic simplicity while supporting a more expressive form of smart contracts than UTXO allows [6].

B. Public Key Cryptography

Public key cryptography (PKC) is built on the cryptographic primitive of Trapdoor Functions, which is a mathematical function that can be solved simply in one direction but is almost impossible to reverse and is integral to every single transaction that occurs on the blockchain [7]. Public key cryptography is used to create an algorithmically linked publicprivate key pair, comparable to a username and password. The private key is used to authorise and sign transactions being sent from the user, creating digital signatures that enforce sender provenance [8]. The public key is used to encrypt a transaction before being broadcast to the entire network to enhance privacy and confidentiality assuring that only the intended private key owner can decrypt and view the data. The keys and public addresses are managed by a wallet, either an application or specialised hardware, that keeps track of private key balances [8].

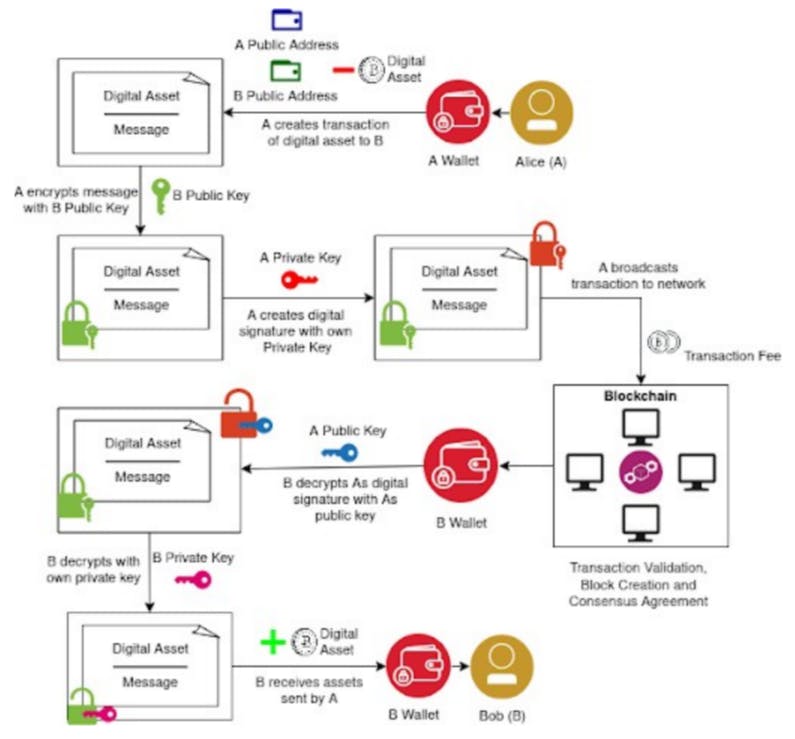
C. Blockchain Transactions

In both the UTXO and account-model transaction systems, sending digital assets to another account on the network follows very similar principles of transaction [9]. Each transaction contains a message with confirmation of both Alice the sender and of Bob the receiver, as well as the value of the digital assets being transacted. Alice will then encrypt and sign the transaction with the relevant keys, and then broadcast the transaction along with a fee to the p2p blockchain network [10]. Validator nodes will select transactions to be validated and generally prefer to maximise revenue from transaction fees. After the block is broadcast, validator nodes will validate that the transaction is viable and accurate then package it into a block with other unconfirmed transactions. This is then broadcast to all other network participants to ensure that the transaction inputs are signed and have not been already spent. When other nodes agree on the validity of a block they will receive a small incentive and the block will be passed along and queued for inclusion in the ledger, eventually coming to a global consensus when enough validators have confirmed the block to be valid [11]. Once the block has been added to the blockchain and confirmed, Bob will then receive the digital asset sent by Alice.

D. Smart Contract

Smart contracts are pieces of coded logic stored within a blockchain network in the form of high-level contractoriented languages to be executed by nodes either manually or when certain conditions are met. Smart contracts contain state storage, specialised logic, a balance and a public/private key address and are capable of receiving assets. Contracts have been integrated into many blockchain networks and serve as part of the core technology enabling transactions to occur in decentralised applications [8]. The implementation of contracts allows more complex transactions of valued assets to occur without censorship, downtime or any centralised third parties to oversee transactions [9] [12].

E. Consensus Mechanism

Consensus mechanisms ensure that nodes within a distributed network stay synchronised and follow a consistent set of rules on how to validate new blocks and achieve Byzantine Fault Tolerance (BFT). BFT is a property of distributed systems that enable the participating nodes to agree on a single strategy to achieve global consensus regardless of failed components or untrustworthy nodes. These mechanisms enable blockchain systems to act in a trustless and decentralised manner, especially when interacting with faulty or malicious nodes [13]. Consensus mechanisms enable large groups of validator nodes to vote upon which block of transactions should be validated in a process called minting [13]. After a block has been minted by a validator and confirmed to coincide with the copy of the ledger currently maintained by them, it is appended to their copy of the ledger and broadcast out, coming to a global consensus on the state of transactions. The weight of a validators vote is proportional to the quantity of resources contributed to the network, with proof-of-work requiring computational power and the proofof-stake consensus relying on tokens pledged to the network. The requirement of resources to achieve consensus is deemed essential, as a “one-node, one-vote” approach could result in many nodes being set up to spoof the network and receive an imbalance of voting power [14].

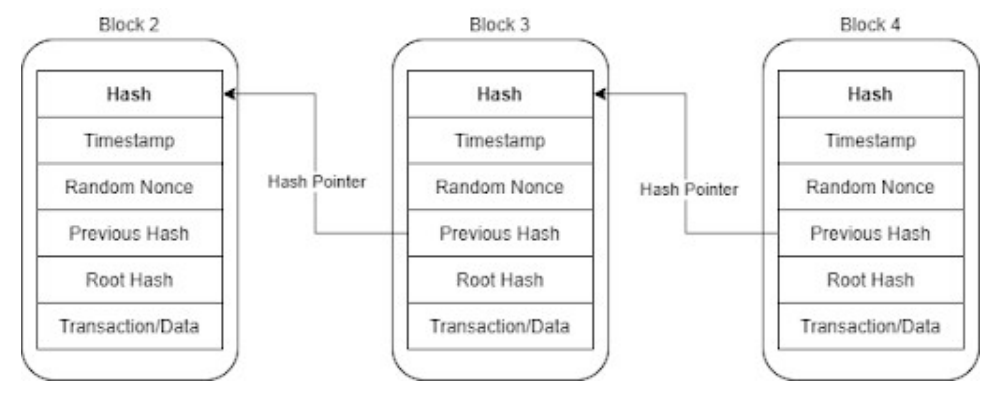
F. Blockchain Structure

Once consensus has been achieved and there have been enough confirmations validating the transactions within the block, the block will be appended to the ledger and broadcast to all nodes to ensure a consistent state. Each block contains a timestamp for when it was appended to the chain, a random nonce (number used once), a merkleized transaction root hash, transaction data, the hash of the previous block and the hash of the current block, which is generated by hashing everything else contained within the block [15]. The previous block’s hash is tethered using a hash pointer, linking each block together in an immutable chain, seen in figure 2. If anything in a previous block is altered it will invalidate the entire chain from that point forward [15].

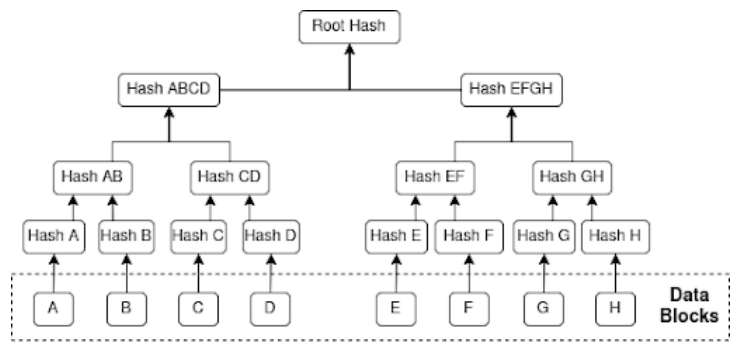
G. Merkle Root Tree

One of the key cryptographic functions utilised in blockchain technology is the Merkle root hash, which is a hash that represents all transactions within a block. The hash values of each transaction are appended together and then further hashed together until a single root hash is formed, as seen in figure 3 [16] [17]. If a singular bit of transaction data is changed within the Merkle tree, the root hash would no longer be valid and the chain would break. This method ensures an immutable and integrity-focused system where any alteration in block data will lead to inconsistency when validating the ledger [11].